Types of Equilibrium


Introduction

Equilibrium is the state of a system in which all forces acting on it are balanced, resulting in no net force or acceleration. Up to this point, we've only discussed equilibrium with respect to forces, but equilibrium can also be defined in terms of energy. Depending on the potential energy of the system, different types of equilibrium may be defined.

We first need to introduce a new few new ideas. First off, the negative slope of a graph of potential energy with respect to position is equivalent to the force acting on the system at that point. Moreover, there is a calculus concept called a critical point. A critical point is when the slope of a function is zero, usually at a local maximum or minimum. These are points where the system is in equilibrium, since the force acting on it is zero.

Recall our formula:

$$ F = -\frac{dU}{dx} $$
As a reminder, this means that the force acting on a system is equal to the negative of the derivative of the potential energy with respect to position. This means that equilibrium points are where this derivative is equal to zero, or where the slope of the potential energy graph is zero.

The way we analyze equilibriums is not by looking at the forces (as one might expect), but rather by looking at the potential energy of the system at and near the equilibrium point. We also won't even be looking much at the slope of the graph, since we know it's going to be zero at the equilibrium. Specifically, we will be looking at the concavity of the graph, which tells us about the nature of the equilibrium point. This lets us define three types of equilibrium: stable, unstable, and neutral.

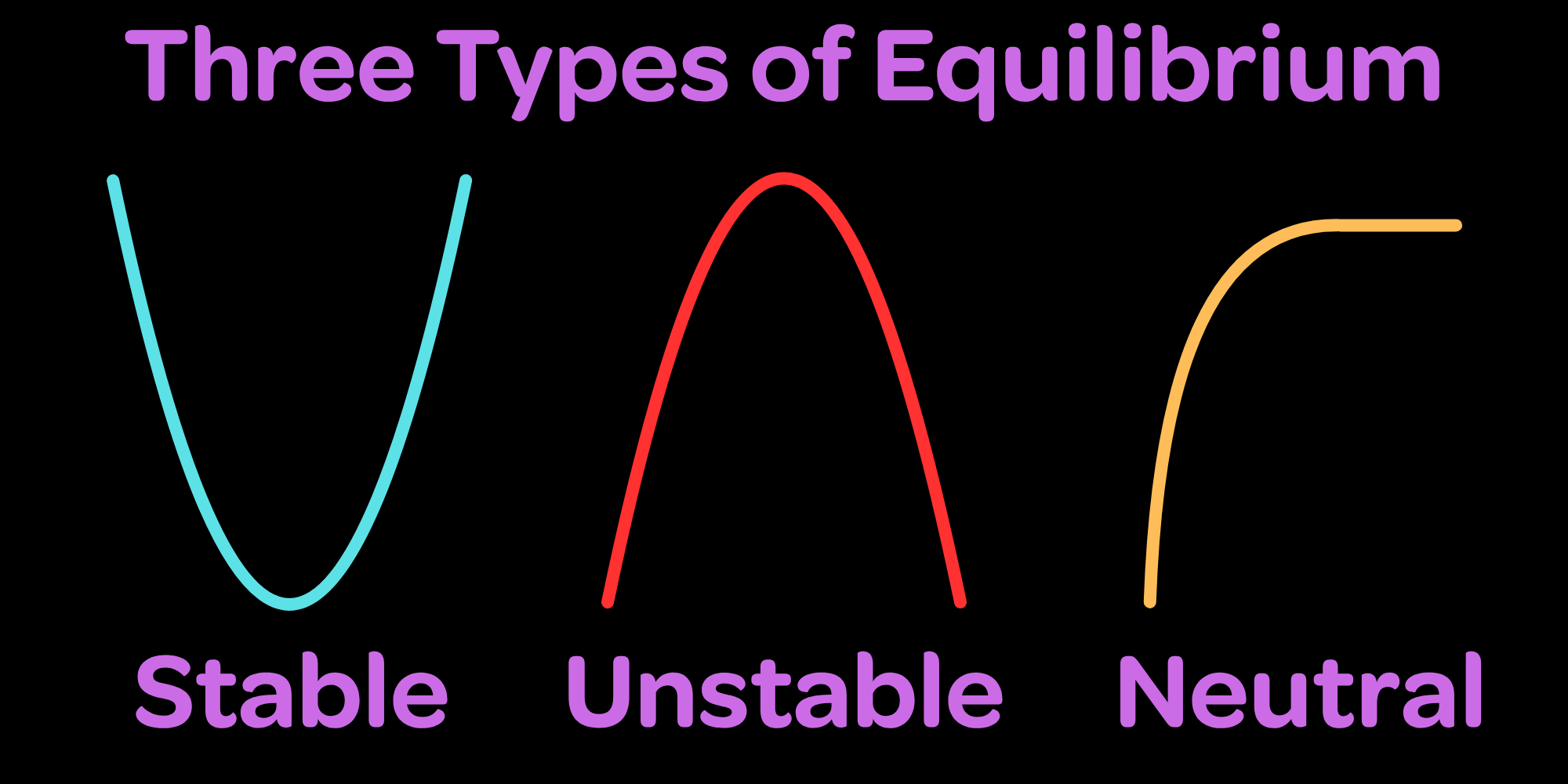
Figure 1: The types of equilibrium. Not sure what compelled me to add a title.

The three types of equilibrium are defined by the shape of the potential energy graph at the equilibrium point. Now, let's look at each of these in detail. This is really supposed to be dependent on calculus, but I'll do my best to explain calculus concepts without actually invoking calculus. It isn't strictly required to know calculus, but this is one of those examples that shows how useful calculus is in physics. This concept is pretty heavily dependent on calculus, as you might have already noticed. For the sake of continuity and simplicity, I won't purely explain it in calculus terms, though you calculus students will have some explanation tailored to you. This lesson is actually really dependent on calculus, though interestingly enough it has a lot of content at a conceptual level that doesn't require calculus. You just need to know how to analyze graphs.

The first thing you should know is that the negative slope of the potential energy versus position graph is equal to the force acting on the system at that point. This is a result that comes from a calculus definition of force, work, and energy, so we won't get into it here. The next thing you should know is a local maximum or minimum is a point where the function is the highest or lowest in a small region around it. These can also be called critical points. This allows us to define three types of equilibrium.

Figure 1: The types of equilibrium. Not sure what compelled me to add a title.
We will get into all of these conceptually in this lesson, without any calculus explanations. It is sufficient to use qualitative analysis, since these really depend on analyzing the shape of the potential energy graph, which is no Herculean task.

Stable Equilibrium

The stable equilibrium is characterized by a local minimum in the potential energy graph. If we look at the graph, we can see that if we displace the system from this point, it will return to the equilibrium point. As an analogy, we can think of the potential energy graph as a graph of height versus position, since gravitational potential energy depends directly on height.

Figure 2: A typical stable equilibrium. The ball is at the bottom of a bowl and will roll back down to the bottom if displaced.

You can think of the ball in the bowl as a good general example, but we aren't always going to deal with gravitational potential energy. The concept is more general than that. There are instances like this in many different systems, such as springs, pendulums, and even more complex systems involving electricity and magnetism. However, some things remain the same for all stable equilibriums regardless of specific circumstances.

If we displace a system that is at stable equilibrium slightly from the equilibrium point, it will roll back down to the equilibrium point, like a ball in a bowl. The forces acting on the ball near this point are restoring forces that will tend to return the system to the equilibrium point. This term will come up again later, so remember it.

In terms of the second derivative of the graph, it is where the concavity of the graph is positive, or where the second derivative is positive. The slope of the graph is increasing in this region, but this isn't really important to our analysis.

Mathematically, we can say the following (though it's often not necessary to say it):

$$ \frac{d^2U}{dx^2} > 0 $$
In general, stable equilibrium is characterized by a local minimum in the potential energy graph. This makes sense, since a system will generally tend to return to a state of lower potential energy, which makes the equilibrium point stable. The system also experiences a restoring force that is oppositely directed to the displacement from the equilibrium point, which should sound similar to the springs we investigated earlier. A stable equilibrium is where the object will tend to return to equilibrium if it is slightly disturbed. This can be thought of as a ball at the bottom of a bowl. If you displace the ball slightly, it will roll back down to the bottom of the bowl. Of course, this isn't the only example, but it is a good one to visualize and covers the concept well.

Figure 2: A typical stable equilibrium. The ball is at the bottom of a bowl and will roll back down to the bottom if displaced.

Like the ball in the bowl, if we displace a system that is at stable equilibrium slightly from the equilibrium point, it will roll back down to the equilibrium point. This indicates that the force acting on the object is in the opposite direction of the displacement from the equilibrium. These kinds of forces are called restoring forces, since they tend to restore the system to the equilibrium point. This term will come up again later, so remember it.

A stable equilibrium is a point that has the lowest potential energy in a small region around it. This explains why the system will tend to return to this point, since objects and systems tend to go towards points of lower potential energy. In math terms, this is a local minimum in the potential energy versus position graph.

Unstable Equilibrium

The unstable equilibrium is, well, unstable. It's characterized by a local maximum rather than minimum in the potential energy graph. Even though the shapes of the graphs are similar, the unstable equilibrium is literally the antithesis of the stable equilibrium. If we displace the system from this point, it will not return to the equilibrium point. Actually, even that's putting it lightly.

Figure 3: A typical unstable equilibrium. The ball is at the top of a hill and will roll down the hill if displaced.

The unstable equilibrium is like a ball at the top of a hill. If you displace the ball slightly, it will roll down the hill away from the equilibrium point. This is because the forces acting on the ball near this point are not restoring forces, but rather forces that tend to push the system away from the equilibrium point. There isn't a term for this kind of force, since it's not as interesting as a restoring force.

In certain cases, the object's distance from the equilibrium point will increase exponentially. A simple case that causes this is the anti-Hooke's law (not the official name), which is a force that is directed in the same direction as the displacement from equilibrium that follows Hooke's Law.

$$F = kx$$
See how there's no negative sign? This means that the force is directed in the same direction as the displacement from equilibrium, which is why it causes the system to move away from the equilibrium point exponentially. This is a pretty specific case, but it is very similar to Hooke's Law, which we covered earlier. Even a small change in the formula can have a big impact on the system's behavior.

In terms of the second derivative of the graph, an unstable equilibrium is located where the concavity of the potential energy graph is negative, or where the second derivative is negative. The slope of the graph is decreasing in this region.

Again, here's the (somewhat unnecessary) mathematical definition:

$$ \frac{d^2U}{dx^2} < 0 $$
In general, unstable equilibrium is characterized by a local maximum in the potential energy graph. This also makes sense according to logic we used before. Systems dislike points of high potential energy, tending to move away to a point of lower potential energy. In the real world, these equilibriums are often short-lived, as the multitude of forces in a real environment will inevitably disturb a system from this unstable equilibrium and cause it to decay to a more stable state. Think of how hard it is to make a card tower. Even breathing on the structure too hard can cause it to collapse.

We typically interchange equilibrium and stability, but this case shows how different the two can be. While at the unstable equilibrium forces are technically balanced, any disturbance will prompt the system to move away from the equilibrium point in a very unstable manner. The term "unstable equilibrium" is therefore not an oxymoron (at least in physics), but rather something that describes everyday scenarios. Thus, equilibrium and stability are not the same thing in physics!

 What's the opposite of stability? Instability! The unstable equilibrium is in many ways the opposite of the stable equilibrium, exhibiting the opposite behavior. The object will "fall" away from equilibrium rather than tending to return to it. A good example of this scenario is the ball on the very top of a hill.

Figure 3: A typical unstable equilibrium. The ball is at the top of a hill and will roll down the hill if displaced.

Because the ball is at a very high point relative to everything around it, it has a lot of potential energy. This is called a local maximum in the potential energy graph. We said before that systems sort of dislike having potential energy, trying to get themselves into the lowest possible potential energy state. This is why the ball will roll away from the equilibrium at the top of the mountain if disturbed: it will seek a position of lower potential energy elsewhere.

This is why this kind of equilibrium is unstable: because the object or system doesn't like to stay at such a point. Most unstable equilibria decay rapidly, since any small external disturbance can cause the fragile state of equilibrium to collapse. Note that equilibrium and stability are not the same thing in physics, even though we sometimes interchange them. It's not true that a system in equilibrium has to be stable, and we've just shown why!

Unstable Equilibrium Demo




Try balancing the pencil on its tip. That's an unstable equilibrium. If you reset the simulation, the pencil will be able to stand on its tip for a short time because the initial conditions are perfect, but eventually even slight calculational approximations done by Matter.js will cause it to slip over and fall. I'll venture to say that it's virtually impossible to stand the pencil back up once it has fallen. Prove me wrong!

Neutral Equilibrium

This is kind of a weird one. You might think that stable and unstable cover all the types of equilibriums since they're opposites of each other, but there is a third, more dull kind of equilibrium. This case pretty much covers all equilibria that are not stable or unstable. Technically, this is an inflection point ($\frac{d^2U}{dx^2}=0$) where concavity changes, but I've found that this definition is a bit misleading. 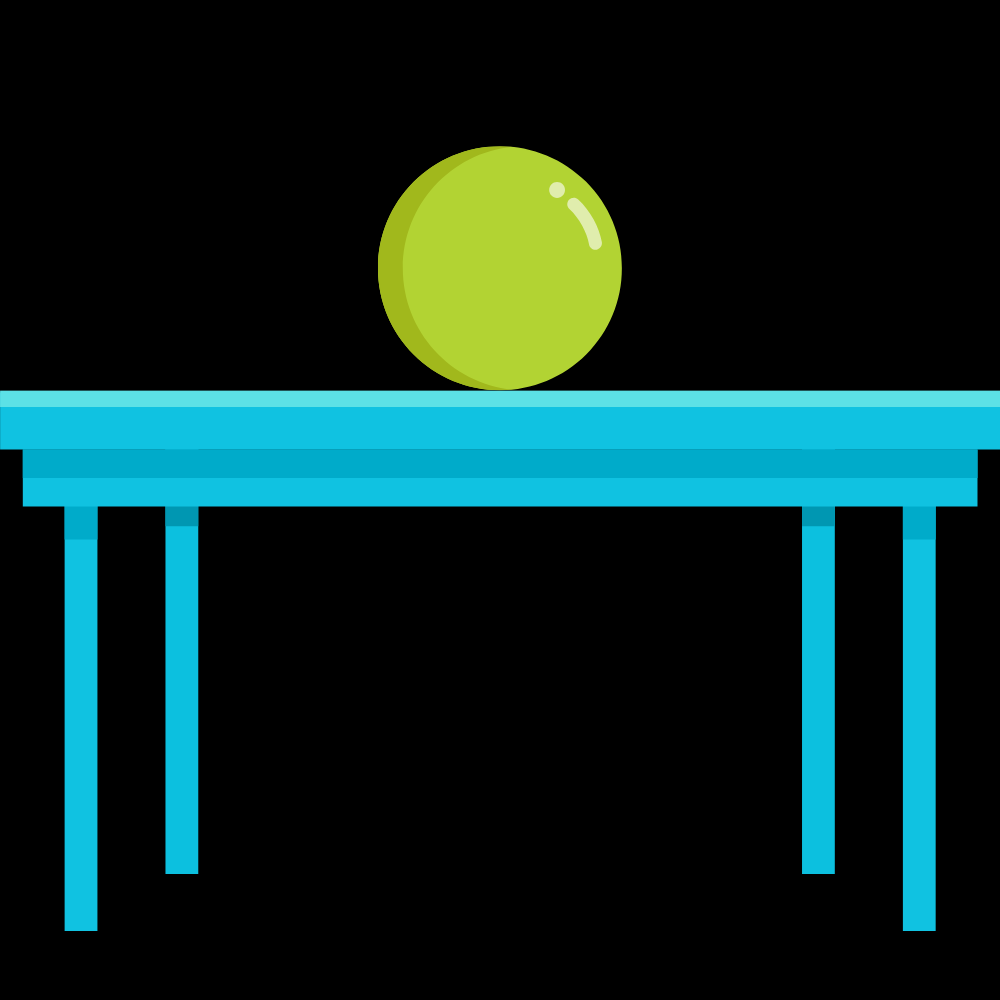In a neutral equilibrium, the system will remain in its new position if disturbed. Let me explain what I mean.

Figure 4: A typical neutral equilibrium. The ball will still be in equilibrium if displaced.

The system will move to a new equilibrium if displaced slightly. It might go back to being at rest, or it could continue on at constant velocity if there are no dissipative forces. For the case of the ball on the table, small displacements will cause it to move around on the table. But, the ball will be at equilibrium at any point on the table, so it will neither accelerate away from nor return to its original position. See what I meant when I said this covers any cases that unstable and stable equilibrium do not?

This kind of equilibrium is characterized by a flat section in the potential energy versus position graph. In the flat section, potential energy doesn't change with position, displacing the object will still result in zero net force being exerted on it. Additionally, there is no tendency for the object to move, as all points around it are at the same potential energy.

While this can be defined as an inflection point, at inflection points the concavity is simply changing, which does not automatically produce a neutral equilibrium. Think of the arbitrarily defined function $U(x) = x^3$, which has an inflection point at $x=0$. If we displace an object at this point to the right, it will eventually end up sliding to the left to negative infinity; the same applies if we displace it to the left. This is not really a neutral equilibrium then!

Moreover, we typically don't think of flat sections as inflection points, but this is what a neutral equilibrium is typically characterized by. Therefore, do not rely on the calculus definition too closely and opt for analyzing the scenario instead.

While this kind of equilibrium is quite common (think of books on a table, boxes placed on the ground, etc.), it is not interesting in the slightest. After all, nothing happens (more precisely, $a=0$) after you displace the object, so the scenario is easy to analyze. It is much more interesting to analyze whether systems are in stable or unstable equilibrium. The neutral equilibrium is NOT a middle point between stable and unstable equilibriums, but something quite different. We can think of it as a ball sitting on a table. If we move it slightly, it will neither roll away from nor return to its original position. Instead, it stays in its new position.

Figure 4: A typical neutral equilibrium. The ball will still be in equilibrium if displaced.

The ball will have the same potential energy at all points close to it, which means that it has no tendency to move or to return. To it, all the position you could displace it to are the same (in terms of energy). This kind of equilibrium is actually pretty common if you think about it. A book placed on its side on a table is in neutral equilibrium.

If a stable equilibrium is a ball wishing to stay and unstable is a ball wishing to leave, then a neutral equilibrium is a ball that is completely indifferent to its predicament. This kind of equilibrium is characterized by flat, horizontal sections in the potential energy graph.
While it is very easy to qualitatively tell what kind of equilibrium a system is in, mathematically the exact analysis unfortunately requires calculus. It's unavoidable, so we will have to deal with this issue by testing your knowledge with conceptual questions. With that said, let's move on to doing a conceptual practice problem where you tell me whether each scenario is a stable, unstable, or neutral equilibrium.


Classify each of the following scenarios as a stable, unstable, or neutral equilibrium. Give reasoning for your answers.

A spacecraft glides through outer space, very far away from any planets or stars.

You stand a coin up on its edge. (Analyze the coin, not yourself!)

A smooth hemisphere is placed on a flat table, with the round face on the table.

A cone tipped onto its side is placed on a flat surface.

A block is attached to a horizontal spring and pulled back slightly.
Calculus is key to calculating whether a particular equilibrium is stable, unstable, or neutral, though in most cases qualitative analysis is good enough. We'll have two practice problems here: one to practice your conceptual understanding of the topic, and one that requires calculus to get through. The conceptual questions are shared between all difficulties (because it would honestly be a waste if I didn't give them to you), but the calculation problem is just for you calculus students. (I bet you feel so special.) We'll start with the conceptual questions to get your neurons firing.


Classify each of the following scenarios as a stable, unstable, or neutral equilibrium. Give reasoning for your answers.

A spacecraft glides through outer space, very far away from any planets or stars.

You stand a coin up on its edge. (Analyze the coin, not yourself!)

A smooth hemisphere is placed on a flat table, with the round face on the table.

A cone tipped onto its side is placed on a flat surface.

A block is attached to a horizontal spring and pulled back slightly.

Hopefully, you have a good grasp on how to quickly analyze which type of equilibrium a scenario is. Most of the time mathematical analysis is not necessary, but to actually prove that a scenario is a particular type of equilibrium it is necessary to use calculus to show that its potential energy satisfies the necessary conditions. This leads us to our calculation problem.

Show that a block of mass $m$ attached to a vertical spring of spring constant $k$ hung from a ceiling is in stable equilibrium.

This might sound easy, but it's actually a little tricky! I'll give a hint. First off, we want to write a general form for the total potential energy in the system. This means that we have to set some point as our zero gravitational potential energy point. Before we do that, however, we should find where this point should be set in order to minimize the amount of calculation we should do.

Did you get it? There are many approaches, so I'll start with the one that's the easiest to understand. For this we'll want to set the zero gravitational potential energy point at the point where the spring is not stretched. Next, we want to find how far the spring would stretch at equilibrium, a quantity which we'll call $x_0$. This involves a bit of force analysis, but it's just setting the gravitational force equal to the spring force.

$$ mg = kx_0 $$ $$ x_0 = \frac{mg}{k} $$
Now, we can proceed to write the total potential energy of the system at this point, taking into consideration that the body sits at rest a distance $x_0$ below the point where the spring is unstretched.

$$ U_0 = \dfrac12 k{x_0}^2 - mg x_0 $$
To verify that we've found the correct equilibrium, we can use the relation $F = -\frac{dU}{dx}$ on this to see if $x_0$ is really a equilibrium.

$$ -\frac {dU}{dx} \big |_{x = x_0} = mg - k x_0 = 0$$
Now, we need to find out what kind of equilibrium this is. This means converting the potential energy in a more general form in terms of just $x$, which can simply be done by replacing $x_0$ with $x$.

$$ U = \dfrac12 kx^2 - mgx $$
Differentiate this twice to get:

$$ \frac{d^2 U}{dx^2} = 2k > 0$$
This value is always positive since $k$ is a positive constant, indicating that the equilibrium at $x= x_0$ is, in fact, a stable equilibrium.

Solution: A mass hung from a vertical spring will be in a state of stable equilibrium at $x=x_0$.

An alternative approach is to define the total potential energy at $x=x_0$ to be zero, allowing us to essentially convert this into a horizontal spring problem. If you could see this, you could've skipped a lot of the work I showed and directly arrived at the answer, but this method is certainly not immediately obvious.

That's it for types of equilibrium! You might have gone into this thinking it should have been in the forces unit, but hopefully you now understand how much it has to do with potential energy. This unit isn't too long or content-heavy, but is important nevertheless. Knowing how to identify each type of equilibrium is an important skill to have in physics, and the topic is pretty interesting. Next, we're going to pivot back to a more familiar concept that most people have heard of: Power. If you're ready, let's move forward!
Next Lesson! →