Newton's Law of Universal Gravitation


Introduction

Isaac Newton knew a ton about forces, but he also investigated gravity. Our concept of gravity to this point is that it's a constant field with field strength $g = 9.81 ~\textrm{m/s}^2$, but this is only true if you're standing on the surface of the Earth. (Technically, this value also varies depending on where you are on Earth.) However, if you go a significant distance upwards, the gravitational force will get weaker.

The Newton apple story is often cited as an instance of Newton "discovering" gravity, but this couldn't be further from the truth. Do you really think people didn't know that objects tended to fall down before then? No, Newton realized that the gravity that causes an apple to fall is the same that causes the moon remain in orbit around the Earth. Take a look at this demo. You can use your mouse to manipulate the "planets", but good luck catching them! Also, do NOT let the bodies clip into each other. They will disappear, and you will have to reset.

Gravity Demo



Gravity

But first, a more rigorous discussion of what gravity really is. We know gravity causes things to fall, so let's start there. Gravity tends to pull bodies closer to each other. This leads us to our first conclusion, that as far as we know gravity is always attractive, tending to pull bodies closer to each other. It also gets weaker with distance, though this might not be entirely obvious since you and I cannot easily go far away from the Earth. (Assuming you don't have access to a rocket.) These are quantitatively summed up by Newton.

From some data he borrowed from Robert Hooke (who later got into an argument with Newton over this exact issue of who deserved the recognition), Newton was able to formulate his Law of Universal Gravitation:

$$F_g = G \dfrac{m_1m_2}{r^2}$$

$G$ is a new constant, the universal gravitation constant, given by $G = 6.67 \times 10^{-11}$. This is a very small value, which explains why it takes something the size of a planet to produce a noticeable gravitational pull. The law is often called the inverse-square law because it depends inversely on the square of the separation between the two bodies. We also introduce a quasi-new quantity, the gravitational field strength:

$$g = G \dfrac{M}{R^2}$$

This measures the gravitational field at a particular distance from an object.

Figure 1: Gravity is what keeps the moon in orbit around the Earth.


I'm going to throw a conceptual question at you here. If the Earth exerts a force $F_g$ on a marble, what force does the marble exert on the Earth? Think carefully before you answer, since your intuition might not serve you perfectly!

The answer is that the marble exerts a force $F$ on the Earth as well! You can thank Newton's third law for that. The Earth is simply too massive to feel any noticeable acceleration from the marble, so we usually don't think of objects exerting a gravitational pull on the Earth.


Shell Theorem

Now, these formulas technically only works for point masses. However, Newton was also kind enough to generalize this to spheres, which are the most common shape for celestial bodies. It is called the shell theorem. This theorem essentially states that the gravitational force from a spherical shell can be treated as coming from its center. A corollary is that there is no gravitational force on a particle inside a spherical shell. The proof of this theorem requires the use of calculus.

Thankfully, you are calculus students. I'll only prove the first part of the theorem since the second is exceedingly complex, and I'll simplify it even further by only considering an object of mass $m$ sitting right on top of a sphere of radius $R$ and mass $M$. Even with these simplifications, the proof is nontrivial.

Split the shell into infinitesimally small rings. Consider the gravitational force from rings on the shell with thickness $dy$.
Figure 2: A visual representation of what I mean.
Now, consider these rings as made up of point particles. Due to symmetry, we know that the net force due to any ring will be downward. The force $dF$ from each ring, with respect to the marked angle $\phi$, is:

$$dF = G m\rho (2\pi x) \dfrac{dy}{(R-y)^2+x^2} \dfrac{R-y}{\sqrt{(R-y)^2+x^2}}$$
Here, $\rho$ is the density of the shell, equal to $\rho = M/4\pi R^2$. The last term comes from the fact that all the force must be directed in the negative y direction due to symmetry. We know that $x = R \cos \phi$ and $y = R \sin \phi$. Since this is a spherical shell, a thin ring along the surface can be approximated as having thickness $dy = dR$. We can thus rewrite the previous equation as:

$$dF = G Mm \dfrac{1}{4\pi R^2} \dfrac{2\pi R \cos \phi R d\phi}{[(R-R\cos \phi)^2+(R \sin \phi)^2]^{3/2}} (R-R\sin \phi)$$
I know this looks complex, but just stick with me and try to keep track of the algebra. I will not be showing every step because that would take absolute ages to write. I'll skip over some basic algebraic steps and leave you to fill in the gaps as an exercise. We are next going to simplify:

$$dF = G \dfrac{Mm}{2R^2} \dfrac{\cos \phi d\phi}{(2-2\sin\phi)^{3/2}} (1-\sin\phi)$$
This can be simplified to:

$$dF = G \dfrac{Mm}{4\sqrt{2}R^2} \dfrac{\cos\phi d\phi}{\sqrt{1-\sin\phi}}$$
Looking at the diagram, we see that we need to integrate from $phi = \pi/2$ to $phi = \pi/2$. We will set these as our bounds of integration:

$$F_g = G \dfrac{Mm}{4\sqrt{2}R^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \dfrac{\cos\phi d\phi}{\sqrt{1-\sin\phi}}$$
This can be solved by using u-substitution, where $u=\sin\phi$. The end result we get is:

$$F_g = G \dfrac{Mm}{4\sqrt{2}R^2} [-2\sqrt{1-\sin\phi}] |_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$$
If we solve, we get an answer of:

$$F_g = G \dfrac{Mm}{2R^2}$$
This is not what we expected! In fact, it is off by a factor of two. Now, we carefully look back and realize that we technically only integrated over one hemisphere, because sweeping from $\phi = - \pi /2$ to $\phi = \pi / 2$ only covers half of the entire sphere. To get the correct answer, we simply multiply this by two:

$$F_g = G \dfrac{Mm}{R^2}$$

This is a loose proof of the shell theorem. The second part is much harder to prove and I won't put you through that.

Now, most celestial bodies are solid spheres and not shells. However, we can treat a sphere as a collection of infinitely many shells, so it all works out in the end. You can apply the first part of the shell theorem to a solid sphere as well, which proves to be quite useful in problems involving many planets or stars that have large radii. Remember to measure the separation $R$ between the centers of the spheres and not the surfaces of the spheres. The theorem isn't really all that revolutionary and mostly follows common intuition.

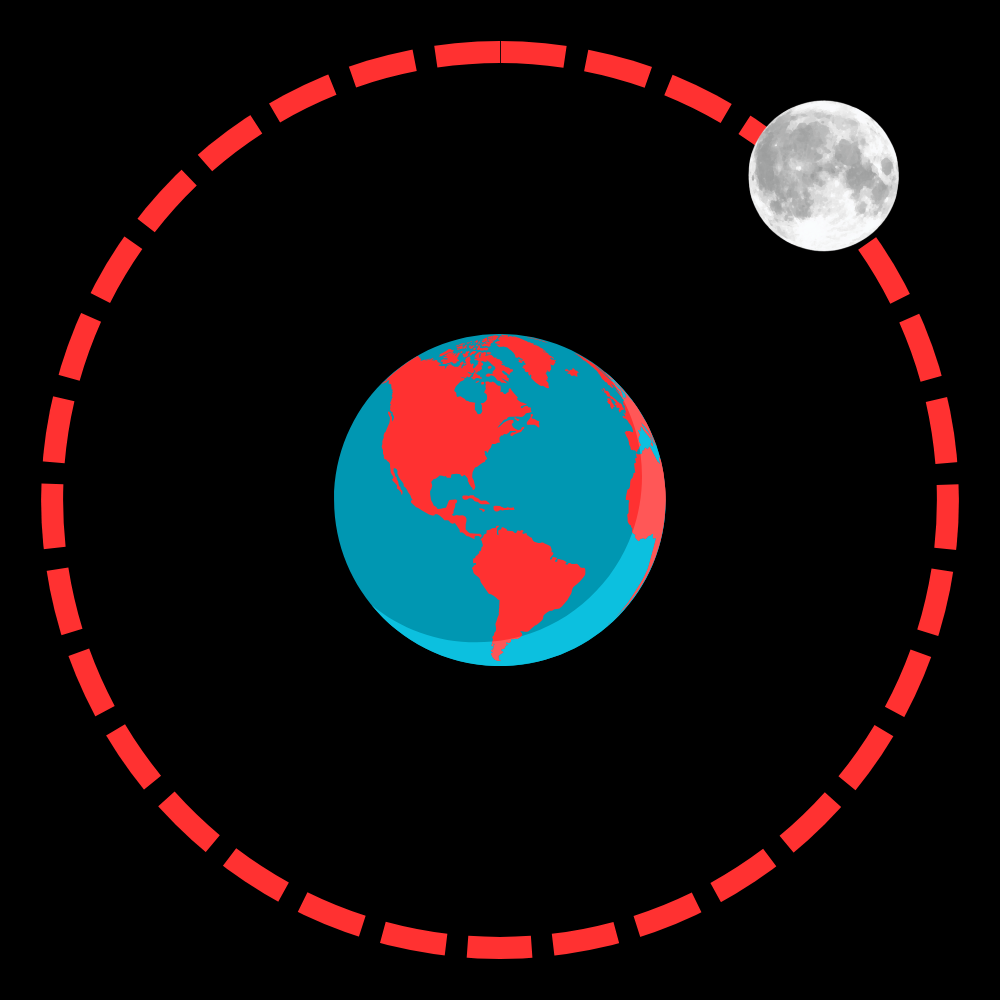
However, there is one interesting case. While gravity outside the planet varies inversely as the square of the distance, inside the planet things are different. We will go over this in the next section. Remember Newton's third law? Well, it still applies here! The Earth exerts a force on you, and you exert that same force back on the Earth. However, the Earth has too much mass to really care, so we usually don't think of ourselves as exerting a gravitational force on the Earth. It's important to remember this fact (which applies to any two objects that have mass), however.

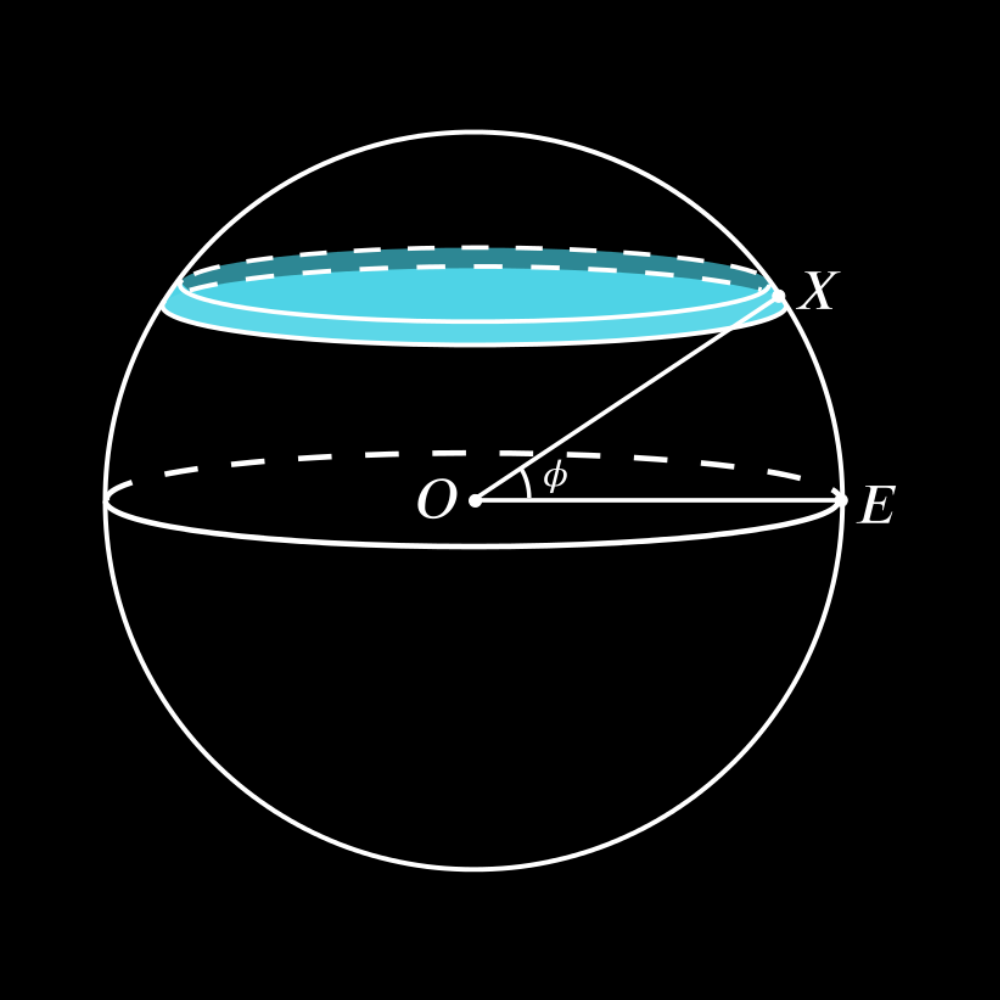
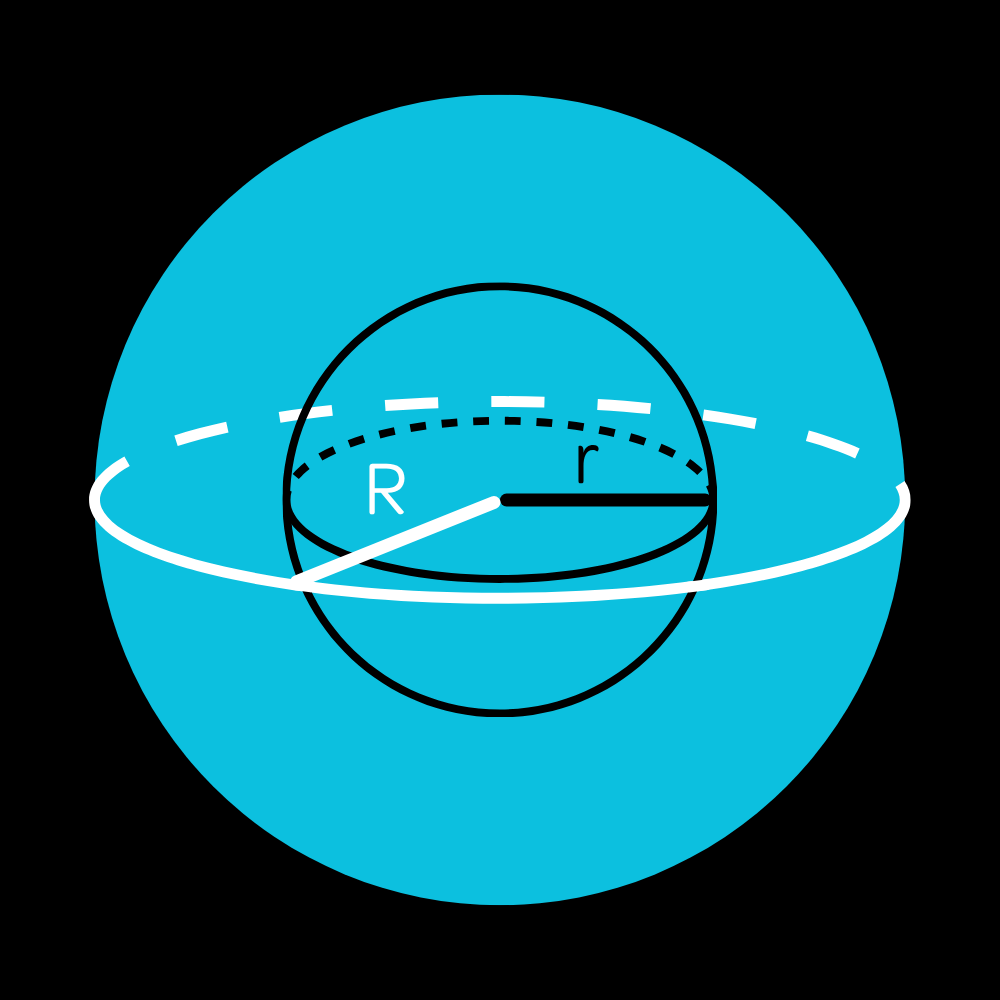
Shell Theorem

Now, there is a theorem called the shell theorem that enables us to treat spheres as just point objects, which allows us to easily use Newton's Law of Universal Gravitation on them. All you need to know at this level is that this theorem allows us to treat a sphere or spherical shell as having all of its mass at its center, and the distance between that center and any other object in question is the separation of the bodies $R$ in the equation.

The one key exception (and the second part of the shell theorem) to this is that there is no gravitational field inside a spherical shell. This makes a sort of sense if you think about it, as the parts of the sphere you're closer to exert a stronger pull but are lesser in area, while the parts further away are more numerous but exert a lesser pull in the other direction, which cancels everthing out.

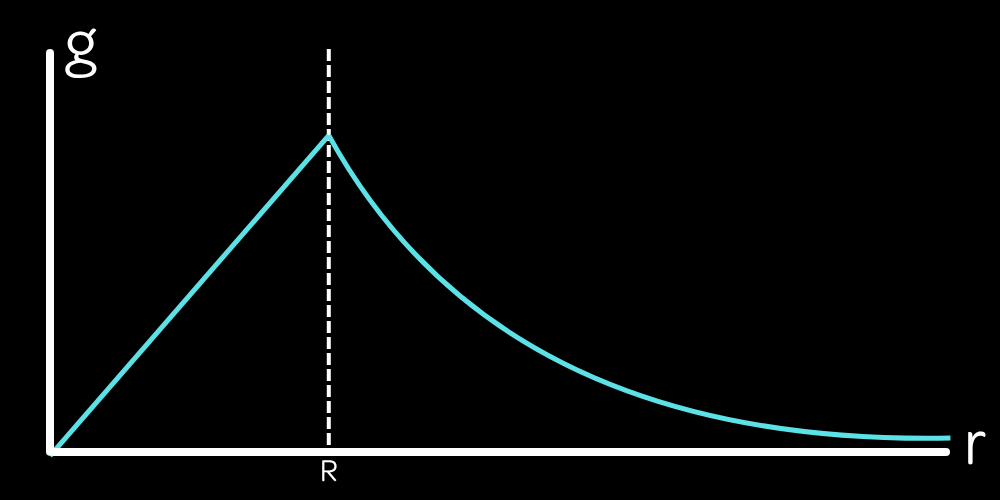
Using this theorem, we can actually figure out what the gravity inside of a planet is.
We can't physically go inside a planet, but thanks to physics we can mathematically do so! This requires the use of the shell theorem, and gives rise to a pretty interesting mathematical result.

Figure 3: A not-so-fortunate soul gets to experience what it's like inside a planet.


Now, what we want to realize is that any part of the planet above you can be considered a series of spherical shells. However, if they're above you, that means you are inside the shells and therefore they exert no gravitational force on you. The only part of the planet that matters, then, is the mass contained within a radius $r < R$, where $R$ is the radius of the planet. Here's a diagram to hopefully make what I'm saying clearer. Only the mass within the black sphere actually matters; anything outside exerts zero net force on any object and contributes zero gravitational field.

Figure 4: The effective mass acting when considering gravity at a distance $r$ from the center of a planet.


Now, to simplify things we'll assume the planet has a uniform density $\rho$. This isn't always true; in fact, planets tend to get denser towards their cores since there is a great pressure from gravity as you go deeper into the planet. Dealing with non-uniform density is quite possible, though it is more complex than is needed for this example.

The mass $m$ enclosed within a radius $r$ can be given by:

$$m = \rho \frac{4}{3}\pi r^3$$
Since $rho = M/(\frac{4}{3}\pi R^3)$, we get the result:

$$m = M \dfrac{r^3}{R^3}$$
Knowing the enclosed mass allows us to use the formula for the gravitational field ($g = G \frac{m}{r^2}$) to directly compute our desired results:

$$g = G \dfrac{M}{R^3} r$$
We see that this indicates that the gravitational field inside a uniform planet is a linear relation, which is quite an interesting result. The field outside follows the inverse-square law but the field at the boundary must be the same. Indeed, when we plug $r=R$ into the expression we get the expected result. Here's a graph of the gravitational field as a function of $r$ from the center of the solid sphere:

Figure 5: The graph of $g$ vs. $r$ for a uniform solid sphere.


Talking about just one object is boring, so next we're going to ramp it up to two objects. That is, we're going to talk about orbits. Gravity inside a planet (which is really just a solid sphere in this case) requires quite a few calculations, so we're just going to conceptually go over the subject without getting into the calculations. First, we have to realize that the sphere is really just a bunch of spherical shells nested inside each other. This means that inside the planet, you have two different parts of the planet that are acting on you. The part "above" you is a bunch of shells that you're inside, so it has no contribution to the field. Only the part "below" you can contribute to the gravitational field you experience. Here's a diagram to show what I mean by "above" and "below".

Figure 4: Everything inside the black sphere is "below" and everything outside is "above". I wish I had better words to explain it.


Now, the mass inside the black sphere is obviously not the entire mass of the planet. We are going to do approximate analysis of this problem by ignoring factors and writing everything as a proportionality such that the math is easier. If we assume the planet has constant density everywhere, this means that the mass $m$ enclosed is proportional to the density times volume, which is proportional to the cube of the radius $r$ of that enclosed sphere:

$m \propto \rho r^3$

The density is proportional to the total mass $M$ divided by the total volume, which is again proportional to the cube of the sphere's radius $R$.

$$\rho \propto \dfrac{M}{R^3}$$

This means that $m$ is proportional to:

$$m \propto M \dfrac{r^3}{R^3}$$ (Actually, it's exactly equal to this because the formulas for the two volumes are the same!)
Then, we can use the gravitational field formula ($g = G \frac{m}{r^2}$ and eliminate all constants like $M$ and $R$ to write:

$$g \propto r$$

This indicates that the gravitational field inside a solid sphere is directly proportional to the distance from the center! This is quite an interesting result. At the boundary point where $r = R$, the gravitational field from this expression and from the inverse-square law have to match up, and if you do all the math they indeed do. To top it all off, here's a generalized graph of the gravitational field as a function of the distance $r$ from the center of the sphere:

Figure 5: The graph of $g$ vs. $r$ for a uniform solid sphere.
We've only talked about the gravity from single objects, but if you're familiar with the solar system you know that there's multiple objects at play. Next, we're going to talk about how the moon and our artificial satellites stay in motion around the Earth due to its gravity, along with many other scenarios for orbits.

Orbits

We just talked about circular motion two lessons ago, so now is a good time to talk about circular motion of planets, more often called orbits. To begin, we'll only talk about circular orbits here because they are easy to deal with, though in our next lesson we will introduce how the circular orbit is an incomplete model.

For our first case, we'll consider a small object like a satellite in a circular orbit around a much larger body such as the Earth. This allows us to essentially ignore the effects of the satellite on the planet because of how much more massive the planet is.

Now, we're going to assume that the satellite has a mass $m$, the planet a mass $M$, and the orbital radius is $R$. This should allow us to write force equations relatively simply. The only force acting on the satellite is the gravitational force from the Earth, and so it must contribute the centripetal force.

$$F_g = m\dfrac{v^2}{R}$$
Note that the orbital radius is measured from the center of the planet. Sometimes, you'll be told how far above the surface of the planet the object is. This is not the orbital radius or the separation between the objects; you would need to add the planetary radius to that height value to get the correct radius. We know the expression for $F_g$, so we can write:

$$G\dfrac{Mm}{R^2} = m \dfrac{v^2}{R}$$
This allows us to eliminate $m$ from both sides of the equation and write:

$$G \dfrac{M}{R^2} = \dfrac{v^2}{R}$$
The only value in this equation that is not known is $v$, so we can solve for that to find the orbital velocity:

$$v = \sqrt{G \dfrac{M}{R}}$$
This actually gives rise to a very interesting conclusion. See, we assumed values of $M$, $m$, and $R$, but we only got back a single value of $v$ that would satisfy the force equations. This means that for each orbital radius, there is only a single possible velocity! Indeed, this makes sense if you think about it. Orbiting near the Earth means you would have to move faster, and orbiting further away means you don't need to move as fast.

The result we derived above is simple, but it is a bit oversimplified in that it only considers the motion of the satellite. If the satellite were instead a planet with comparable mass to the Earth, we would have to consider the motion of both bodies. The easiest case to deal with is a binary system, with two identically massed objects orbiting each other.

Figure 6: A binary system of two identical bodies.


The first thing to know is that whenever two planets orbit each other, they will orbit about their center of mass. They are also always positioned such that they are diametrically opposed. For our particular scenario, the center of mass is exactly halfway between the planets because they have the same mass, making our calculations much easier. Denoting the mass of each planet as $m$ and their total separation as $R$, we can write:

$$G \dfrac{m^2}{R^2} = m \dfrac{v^2}{R/2}$$
This allows us to write the result:

$$v = \sqrt{G \dfrac{m}{2R}}$$
Note that this is a very specific result and only applies if the two bodies are identical in mass! Many scenarios will have the bodies have different masses, and while the overall approach is similar the result most definitely is not. Moreover, it's important to be careful in reading the question, as they may give you the orbital radius instead of the separation of the bodies.

This generalized problem is known as the two-body problem, and was solved completely by Newton. However, when Newton attempted to generalize this to three bodies in what is called the three-body problem (also a book, but that's something entirely unrelated), he found that he was unable to solve it. He chalked this up to insufficient mathematical prowess, but now we know that it is actually unsovable in most cases and requires direct computation by computers to actually solve. Why am I telling you this? Well, for one I think it's interesting. But also, I want to emphasize that this two-body scenario is as complex as most problems will get, though there are numerous variations on the scenario.

Figure 7: One specific "solution" to the three body problem given certain initial conditions. Credit to Wikimedia.

Conclusion

Next, we will talk about real planetary motion, which differs quite a bit from the circular orbits we have talked about here. So without further ado, let's jump into the world of Kepler's laws, which have astronomical importance. There is math behind this, but we won't be too concerned with it here. Instead, we will reason through the results with qualitative analysis. First, we know that gravity gets weaker as the inverse of the square of separation $1/R^2$. Since the orbit is circular and gravity is the only force on the satellite, it must provide the centripetal force, which gets weaker as the inverse of the separation $1/R$. This allows us to write:

$$\dfrac{1}{R^2} \propto \dfrac{v^2}{R}$$
Doing some simple algebra tells us:

$$v \propto \sqrt{\dfrac{1}{R}}$$
What this result tells us is that there is only a single possible velocity for a circular orbit at any radius $R$ from the center of the planet! In most cases, the velocities for a given value of $R$ can be changed, but this is not the case for planetary orbits. This result is used in practice by geostationary satellites, which orbit at just the right altitude such that their orbital time is equal to 24 hours.

Now, what if the masses of the two objects were more similar? Well, this is what we call a binary system, and it exists in nature. Sometimes, two stars will become attracted by gravity and orbit each other in what is called a binary star system. However, for our purposes, it is sufficient to deal with two objects that have the same mass.

Figure 6: A binary system of two identical bodies.


The first thing you might notice is the red x marking the center of mass. Indeed, in systems like this the two bodies always orbit around their center of mass, even though there is technically nothing at the center of mass. The next thing you should notice is that each body is on either side of a diameter of the circle that describes their orbit. In other words, they are always 180° away from each other. This is also always true in all scenarios. But why did I make both masses identical? Well, it simplifies things.

Since both masses are identical, the situation can be significantly simplified. We have the center of mass exactly halfway between the two bodies, and each one's orbital radius is equal to exactly half of the separation between them as a result. They will also both orbit at the same speed. None of these are true generally, but rather arise because of the symmetry of this situation. If the two masses were different, more analysis would have to be done to determine details. At a conceptual level, it's not essential to know exactly how to compute this.

Now, we've discussed only circular orbits, but a certain German man actually discovered that this wasn't the case for real planets. He formulated three laws of planetary motion, which are the key focus of our next lesson. So if you're ready, let's jump right in.
Next Lesson! →